作成AG: ddhhtxvg
(2022/05/18 公開, 2023/11/30 更新)
最近は自分なりの多重の作り方を絞っており, ここに書いてみることにした. ここで扱うのは, 3つのポータルでCF (Control Field)を1つ作成する場合に, その内部に含まれるポータルを用いて多重化する方法である. 多重 CF につい て勉強するにあたり, こちら[1, 2]を参考にした. また, 「完全多重」は人によって定義が異なったり, 「フラクタル」がCF 作成 の呼称となっているようなので用いない. 本来は幾何学における概念を指すは ずである. ここでは次のように定義して用いることにする.
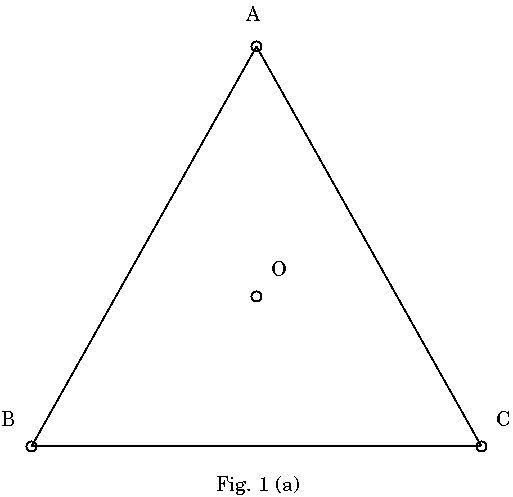
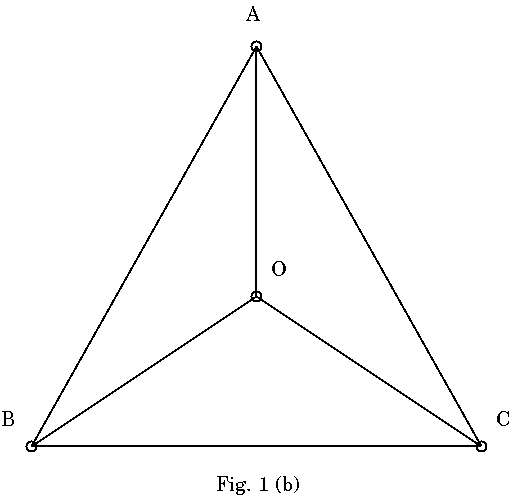
まずはリンクの方向と構築の順序を無視して考える. Fig.1(a)のように, 頂点 ポータルA, B, CによるCFの中に, 未使用ポータルOがあったとする. このとき 多重化しようとしたら, Fig.1(b)のようにA, B, CとOの間にリンクを張ればよ いことになる. このとき新たに生成されるCFはABO, BCO, CAOの3つで, 2重化 したことになる. これはよくある方法にすぎないが, ここで紹介する考え方は, 1つの三角の中の未使用ポータル1つを使って多重度を1上げる, という基本であ る.


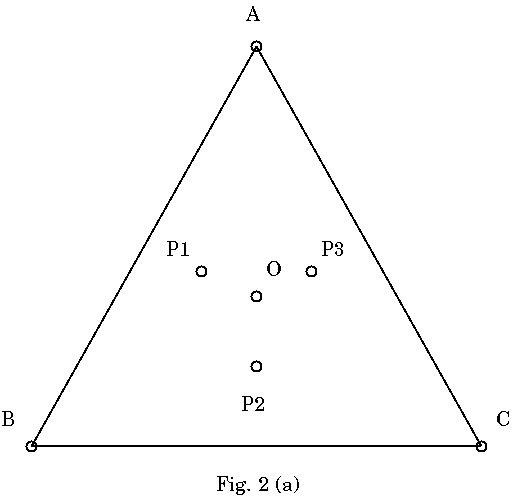
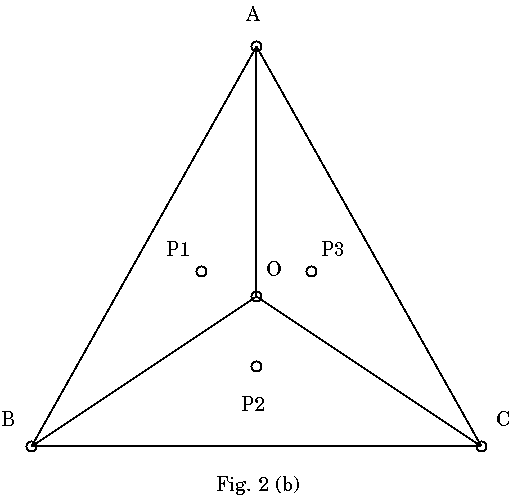
では次にFig.2(a)のような, 頂点ポータルA, B, CによるCFの中に, 未使用 ポータルOと, P1, P2, P3があった場合を考えてみる. Fig.2(b)に示す通り, 頂点A, B, CとOとの間にリンクを張って多重度を1上げるところまでは上記の場 合と同じである. その後たまたま各CFの中に未使用ポータルP1, P2, P3があっ たらどうなるか. Fig.2(b)のようにABOの中にP1, BCOの中にP2, CAOの中にP3 がある. それぞれのCFの中に一つだけ未使用ポータルがあることになる. Fig.2(c)のように, 中のポータルと, それを囲む最小の三角の頂点との間にリ ンクを張れば, 上記と同じ理屈でそれぞれの三角の中に新たにCFを3つずつ生 成,多重度を1上げることができる.
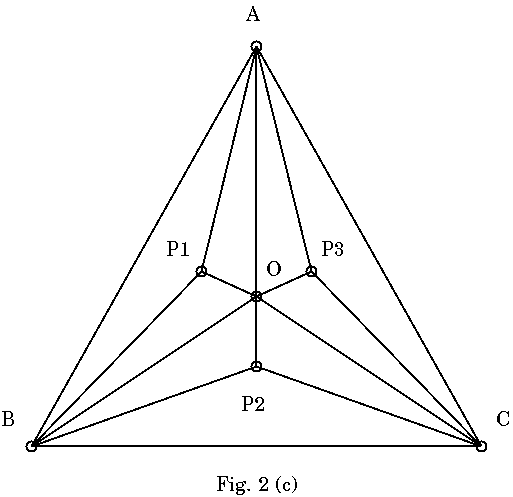
というわで, 1つのCF内の未使用ポータルを1つだけ使ってリンクを3本張れ ば,新たにCFを3つ生成, 多重度を1上げることができる. このようにして, 1つ 未使用ポータルを消化し, 新たに生成された3つのCF内のさらに内側の未使用ポー タルを同様にしてCF生成に使ってゆくことになる. 頂点A, B, Cについてはそ れぞれ1本ずつ鍵が必要, 内部のポータルO, P1, P2, P3については, 囲まれて いる三角を3本のリンクで3つに割ることになるので, 内部のポータル1つについ て鍵は3本ずつ必要ということになる.
さて, 実際の作り方であるが, ここで紹介する方法はポータルをCFで沈めて おいて後から内部へリンクを飛ばす方法となるので, 内部に作成する構造は先 に作成しておく必要がある.
気をつけなければいけない原則は次の3点である.
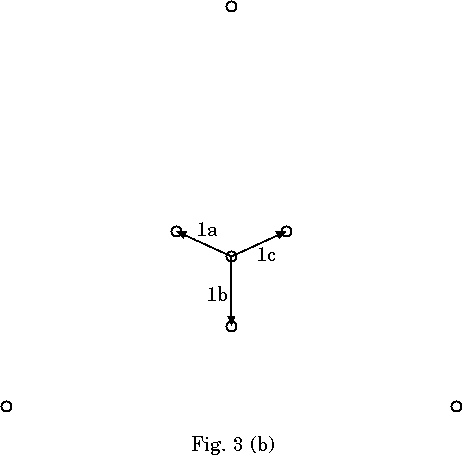
これに従って作成の手順を, Fig.3(a)〜(f)に示す. 各リンクの順序は守ら なくていいところと守らなければならないところがある. 例えばリンク4a〜 4fの順序は入れかわっても問題ないが, 3bと4aが逆になるとこの部分は多重に ならない. また, 外側の頂点の成すCFで内側を沈めてから内部を割ってゆく必 要もない. 何周もするのはめんどくさいし. 例えば, 2a, 2b, 3c, 4c, 4d, 2c, 3a, 4e, 4f, 3b, 4a, 4bの順でも可能である.
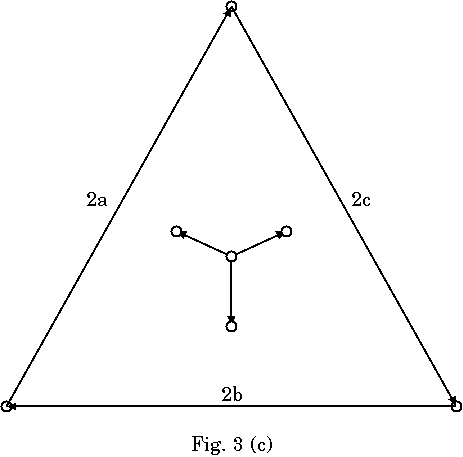
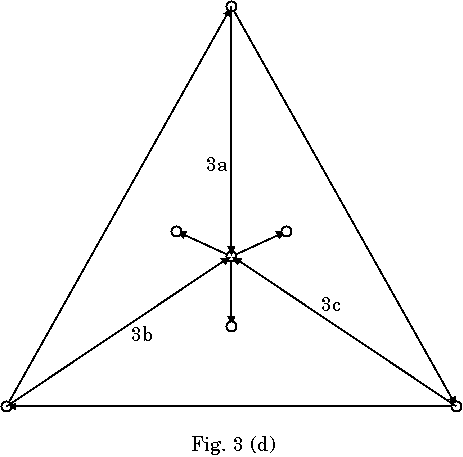
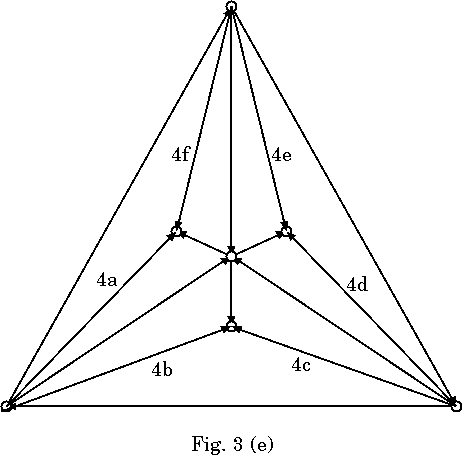
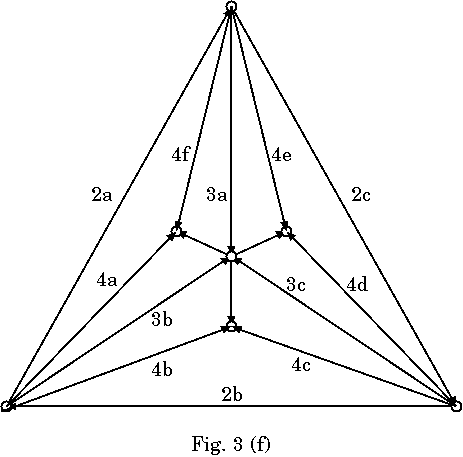
この作成法の問題点は, ポータルOとA, B, Cのアウトリンクが増えやすくハ ブ化しやすいことである. 1ポータル3鍵の原則は崩れるが, リンクの向きを工 夫するなどの方法でアウトリンク数の増加については若干の回避は可能である.
以上のように考えると, 完全多重で使用する内部ポータル数は次のようにな る.
内部ポータル数: \(N\)
内部リンク数: \(3N\)
内部CF数: \(3N+1\)
また, 完全均一多重の多重度と使用する内部ポータル数の関係は,
多重度: \(n\)
内部ポータル数: \({\displaystyle \sum^{n-1}_{k=1}3^{k-1}}\) (ただし \(n\ge 2\))
となる.
参考文献:
更新履歴: